
¿Eres de esas personas que quiere tirar su trabajo por la borda y sueña con ganarse la lotería para vivir sin preocupaciones y con mucho ocio?, entonces debes leer lo que dice este estudio de la Universidad de Manchester.
¿Cuántos billetes de lotería necesita comprar para garantizar ganar algo en la Lotería?, esa fue la pregunta que trataron de responder los matemáticos.
Centrándose en el juego insignia de la Lotería Nacional ‘Lotto’ del Reino Unido, que extrae seis números aleatorios del 1 al 59, el Dr. David Stewart y el Dr. David Cushing descubrieron que 27 es el menor número posible de boletos necesarios para garantizar una victoria, aunque, lo que es más importante, sin garantía de ganancias.

Describen la solución utilizando un sistema matemático llamado geometría finita, que se centra alrededor de una estructura triangular llamada plano de Fano. Cada punto de la estructura se traza con pares de números y se conecta con líneas: cada línea genera un conjunto de seis números, lo que equivale a un boleto.
Se necesitan tres planos Fano y dos triángulos para cubrir los 59 números y generar 27 conjuntos de boletos.
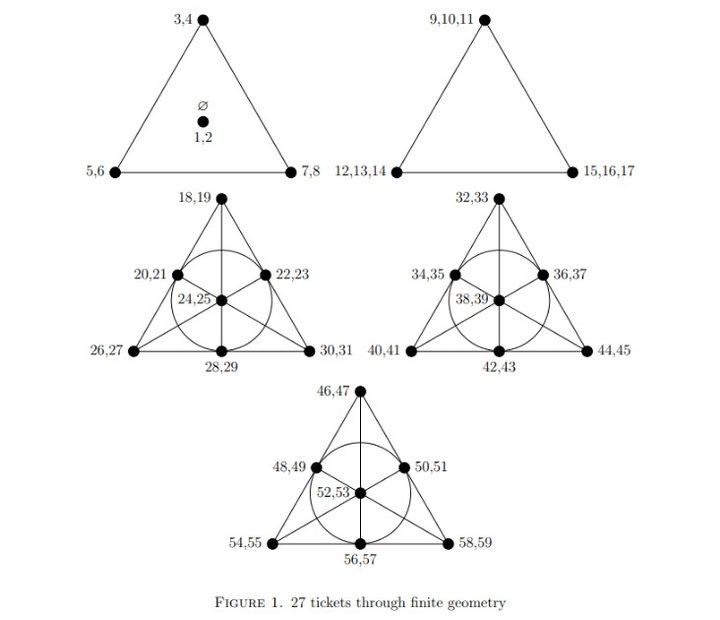
Elegir las entradas de esta manera garantiza que no importa cuál de los 45.057.474 posibles sorteos se produzca, al menos una de las entradas tendrá al menos dos números en común. De cualquier sorteo de seis, dos números deben aparecer en una de las cinco estructuras geométricas, lo que garantiza que aparezcan en al menos un boleto.
Pero el Dr. Stewart y el Dr. Cushing dicen que el trabajo duro en realidad está demostrando que lograr el mismo resultado con 26 boletos no es posible.
El Dr. David Stewart, lector de matemáticas puras en la Universidad de Manchester, dijo: «Fundamentalmente hay una tensión que proviene del hecho de que solo hay 156 entradas en 26 boletos. Esto significa que muchos números no pueden aparecer muchas veces. Eventualmente verás que podrás encontrar seis números que no aparecen en ningún boleto juntos. En términos de teoría de grafos, terminamos probando la existencia de un conjunto independiente de tamaño seis».
Aunque se garantiza una victoria, los investigadores dicen que las posibilidades de obtener ganancias son muy poco probables y no deben usarse como una razón para apostar.




